1年で日本医科大学に合格!
「理解できるまで追求する授業のおかげです」
日本医科大学 医学部医学科合格 長瀬さん(三鷹市在住/19歳男性/既卒生)
特に数学に関しては、自分が一つ答えを出すと、先生が別解を作成してくれました。参考書に書いてある解答のほかにも、さまざまな別解を教えてくれたので、一つの問題...


医学部受験する家庭が最も信頼する
『プレジデントファミリー』で紹介
逆転合格に強い個別指導塾として、フルカラー1ページでTHE MATH運営元であるアシリが掲載。「塾業界は口コミ、評判が悪い有名塾も多い中で、ネガティブな評判がなく、攻めの個別指導が強みの塾である」として評価いただきました。

【2026/2/1更新】
物理2名、化学2名の募集を再開しております。(2026/2/1更新)
3月より入会を検討されている方はお早めに体験授業をお申込みください。
※初回の授業は2月下旬以降の開始になります。それ以前の開始についてはご相談ください。
※曜日・時間帯の指定はできませんのでご了承ください。
.png)
 典型問題の解法を暗記すれば入試でも高得点が取れると思っている。
典型問題の解法を暗記すれば入試でも高得点が取れると思っている。 覚えることが効率的だと思っている。
覚えることが効率的だと思っている。 わからなかったらすぐに解答を見てそのまま解答を書き写している。
わからなかったらすぐに解答を見てそのまま解答を書き写している。 チャート式を3周して完璧にすれば学力が上がると思っている。
チャート式を3周して完璧にすれば学力が上がると思っている。.png)
.png)
.png)
 言葉の正しい定義を覚え、公式・定理は必ず自分で導けるようにする。
言葉の正しい定義を覚え、公式・定理は必ず自分で導けるようにする。 決して問題のパターンを覚えようとしない。
決して問題のパターンを覚えようとしない。 単元の繋がりを意識した体系的な理解を目指す。
単元の繋がりを意識した体系的な理解を目指す。 試行錯誤して問題を解く時間そのものが実力がつく時間だと認識している(安易に解答を見過ぎない)
試行錯誤して問題を解く時間そのものが実力がつく時間だと認識している(安易に解答を見過ぎない)中高一貫の学校であれば、数学IIICまでの範囲の学習を夏から秋にかけて終えるのが一般的です。しかし、その後に数学IAIIBの復習をし、実際の入試問題を解けるようになるためには、半年程度の期間では間に合いません。遅くとも高校二年生のうちには数学IIICの学習を終え、その後に余裕をもって受験対策に臨むことが必要です。
数学の本質的な学習法にも早くから慣れる必要があります。典型的な問題の解法を知っておくのは、もちろん入試において大切なことですが、それだけでは決して全ての問題が解けるようになるわけではありません。数学の得意な人というのは、その解法に用いた公式がなぜ成り立つのか、なぜその解法を選んだのか、その答えは本当に正しいのか、といったことに対する回答を持っています。
標準的な医学部であれば数学においては高得点を取ることが求められ、難関大理系学部においては難易度の高い初見の問題に対応することが求められます。いずれにせよ、「自分が知っている問題だけが解けて、知らない問題が出たら解けない」という状態では安心して受験に臨むことはできません。知っている問題は受験生なら誰しもが解けるため、差がつきにくいからです。仮にどんな問題が出たとしても、その場で自分で考え、初見の問題に対応する力が必要となります。
1
まずは定義・公式・定理を人に説明できるレベルになるまで徹底的に理解してもらいます。「この定義があるから、計算がこうなる」「この公式の証明がこうだから、この場面で使う」というように、それまで丸暗記していた公式に対する必然性を感じ、理解が伴うことで、使える知識に昇華します。 基礎・基本の理解が曖昧だと、後々偏差値の上がりにくくなってしまいます。
標準的なレベルの典型問題に取り組みます。Tier.1で思考の土台ができていると、なぜそのように解くのかが理解することができます。また、一つの問題に対して、分野を横断して複数の解法で取り組みます。
実際の入試問題のうち初見の問題に取り組みます。初見の問題を見たときに、どのように考え、どのように解答の方針を立てるのかを学びます。典型的な問題パターンを知っているだけでは、初見の問題には全く歯が立たないので、まずは試行錯誤をすることで問題内容を適切に把握する必要があります。初見の問題への対応を知ることで、模試や過去問題における点数が上下することなく、安定して得点を重ねることができるようになります。
高いレベルに達するために知っておいた方が良い知識を扱います。教科書では扱われていませんが、上位大学の受験ではより深い部分まで数学を理解しておく必要あります。様々な単元の繋がりを把握し、一つの問題に対して複数のアプローチができることを目指します。また、実際の入試において答案の記述が数学的に曖昧だと、仮に答えが合っていても満点が取れるわけではありません。自分がどのようにしてその答えに辿り着いたのかを論理的に記述する力を育成し、模試の点数でも正確に判断できない部分を仕上げます。
2
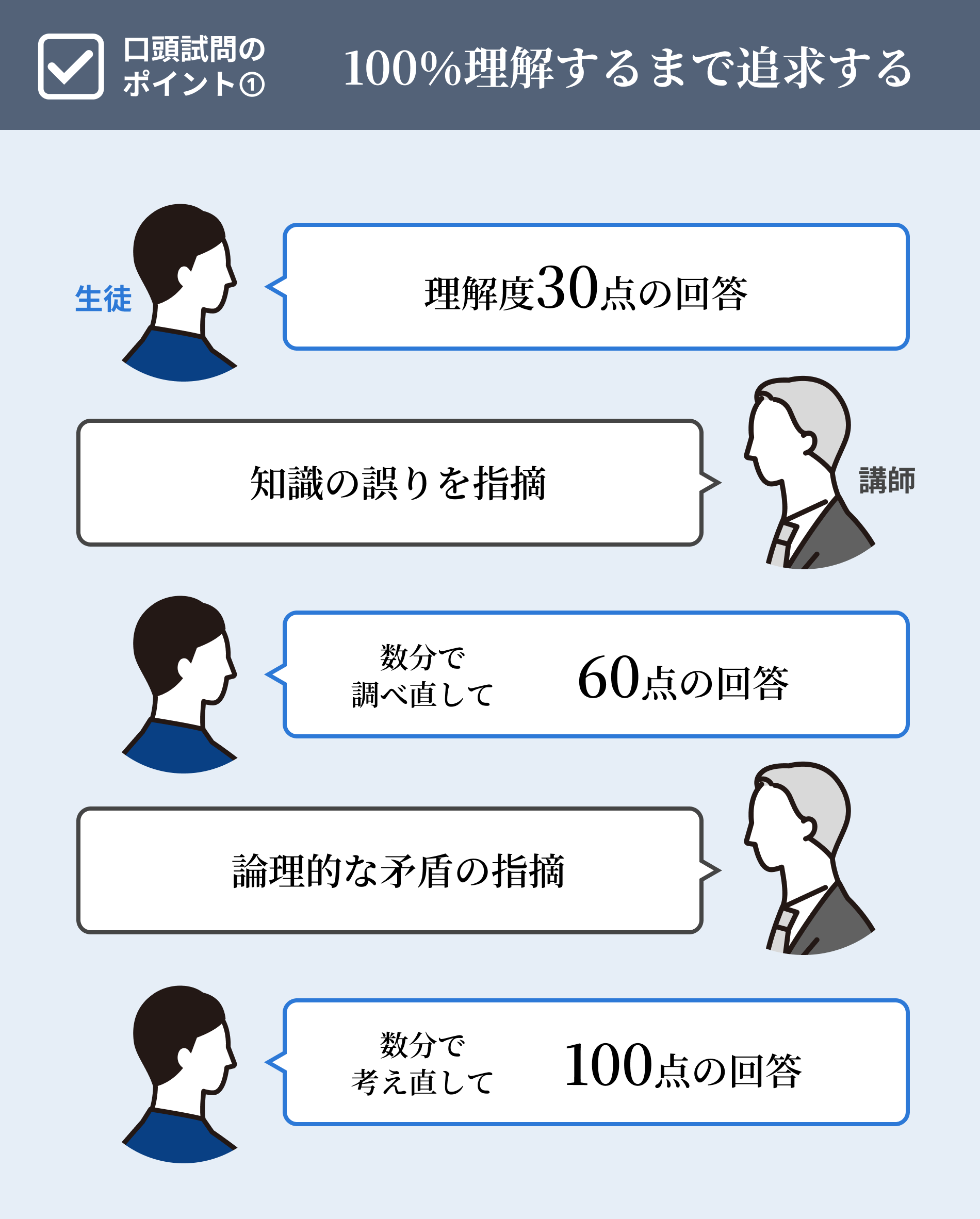
暗記で解くのではなく、思考力を高めて解く授業と口頭試問で、誤魔化しの利かない本質的な理解を促します。生徒の返答はたいていの場合、0点の回答ではありません。一部が正しくて一部が間違っているということが多いです。初めは30点の返答でも、不足している知識が何か気づくように、追加質問をすることで、自律的に60点、80点になっていき、最終的に100点の解答にたどり着きます。
ボトルネックはどこか。全体のうち、どの部分に思考の誤りがあるのか。口頭試問によりあぶり出します。正しい部分は認められ、誤っている部分のみに焦点の当たる指導は効率的で、自力で正解まで辿り着くプロセスが、結果的に、知識の深い理解につながり、深く記憶に刻み込まれることになります。
また、論点を整理する癖がつき、最低限の知識で難問を解ける学力につながるのです。物理化学の入試問題のほとんどは、「どのように工夫して典型問題をそうと見せないようにしているか」で作られているのです。
数学は「問題演習」だけで解けるようになりません。典型問題の解法を丸暗記して定期試験で得点をとることができても、難関大の入試問題は解けるようにはなりません。数学はその科目の特性上、問題演習だけを続けていても、基礎の理解がないと、初見の問題に対応できないという問題にぶつかります。それゆえ、「基本の理解」から始める習慣がない生徒に対して、公式・原則・背景をきちんと理解するまで追求する指導をして、習慣の改善を図ります。そうして、ようやく苦手を克服し、数学の入試問題が解けるようになっていくのです
そもそも、いきなり複合的な典型問題を扱ったとしても、事前に経験しておくべき基礎が固まっていなければ、効果がありません。体操で例えるなら、「バク転」を突然やらせるようなもので、事前の練習が足りないとできません。手首や腕の回し方を一つずつ練習して、初めて複合的な動きであるバク転ができるようになります。基本を無意識に行えるようにすることが、後々効いてくるのは理系科目の勉強でも同じなのです。
数学に関して言えば、実は「覚えておかなければいけないような知識」はほとんどありません。問題を解くことを繰り返しているうちに、「無意識に使い方が自然に身についている」と感じるのが正しい感覚です。「公式や定理の使い方が自然にでてこない」間は、いつも定義から導く必要があり、それを繰り返しているうちに、自然と公式や定理を使いこなせるようになっていくのです。この感覚を得られていない時点で、難問を解くレベルの土俵にすら達していないのです。
「典型問題の解法パターンを暗記すればできるようになるはず」という誤解が非常に多いのが数学の特徴です。もちろん典型問題の解法を知っておくのは大事なことですが、それでは初見の問題に対応することができません。数学の基礎理解の次のステップとして「 (なぞなぞ型) 」で、問題演習の訓練をする必要があります。
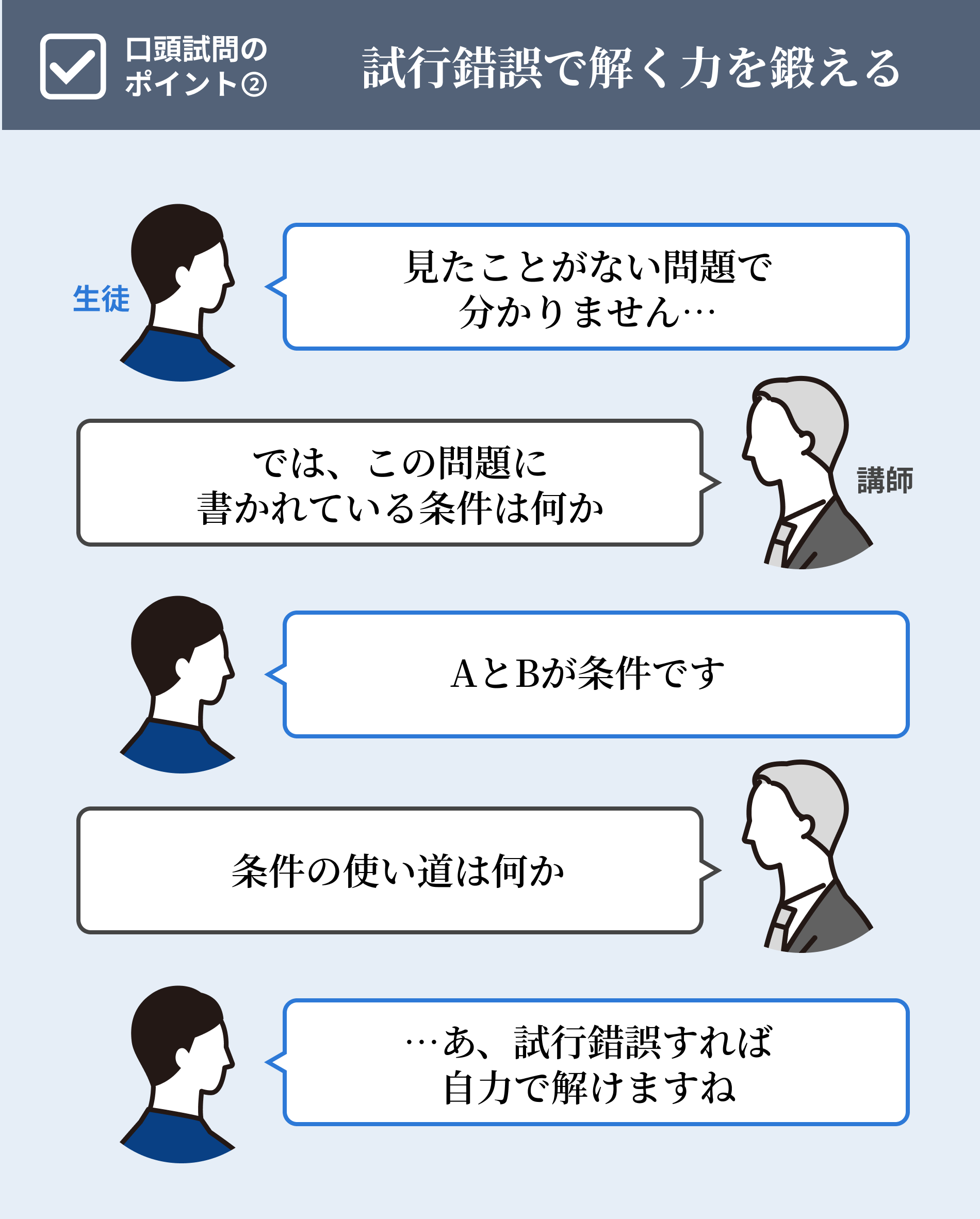
「 (なぞなぞ型) 」とは、すぐに解答が思いつかなくてもなぞなぞと同じように、考え続けることです。初見の問題を見たときには、解答の方針がわからないのが普通で、仮に解答の方針がすぐに思いついたとしても、そのような問題では他の受験生に差をつけることはできません。しかし、苦手な生徒に限って、解けない問題に出会ったときにすぐに解答を見てしまう習慣がついてしまっています。
すなわち、パッと問題を見ただけで、すぐに解答が思い浮かばなかったら解答を見てしまうのは、数学的な思考力を伸ばす機会を自ら失ってしまっているのです。わからない問題に出会ったときこそ、実験を繰り返し、具体的な例を当てはめるなどして、問題の本質的な部分に少しずつ迫る訓練をする必要があるのです。
実際に数学対策で過去の生徒からよく言われてきたのが次のセリフ。
「一旦、有名予備校の人気の授業で対策します」
これらの「有名どころの予備校を使えば大丈夫」という安易な発想が横行しています。しかし、これでは必要な思考力が鍛えられません。そして、難関大を目指すには既に手遅れになった頃に気がつき、個別指導に駆け込む受験生が非常に多いのが現実です。
一般的な予備校における数学の学習の流れは、講師が問題を解説しているのを聞いて類題を自分で解くというものです。全く同じ問題が入試に出ればよいですが、実際にはそうではありません。一つの問題に対するエレガントな解法を知っても、「なぜ自分の解き方ではダメなのか」という疑問が解消されないため、別の問題に出会ったときに手も足も出なくなってしまいます。一つの問題に対して複数の解法を用意し、それぞれの解法についての良い点悪い点を理解した上で、最も適切な解法を選択することが必要です。
特に高校三年生になってから伸び悩みが発覚しても、理系では数学IAIIBIIICと非常に膨大な量を習得する必要があるため、受験戦略上の取り戻せないミスとなってしまうのです。定期試験と同様に、与えられた問題だけ解けるようにしておけばよい、というイメージがあると命取りです。難関大対策では、基本・基礎から理解し直しが必要だと捉えるべきです。
大手予備校の集団授業・映像授業だけでは、苦手から脱却できないのが現実です。成果の分かりやすいテストで、効果があるように見せますが、実際の模試では成績が伸びていないケースが多々見られます。大手予備校の授業の限られた時間で扱う問題数では、どうしても限りがあります。
.png)
口頭試問とは、表面的な理解で終わらせないために、一問一答で生徒の本質的な理解を追求する指導スタイル。
基礎(公式・原則・背景)の理解、徹底だけでなく、難易度の高い問題に対しても深く理解するためにも有効な手段なのです。
.png)
.png)
英語などの文系科目は、「知識量」に比例して成績が伸びる側面がありますが、数学は「思考力」を鍛える必要があり、この「思考力」が何かわかっていないために伸び悩む生徒が多いのです。なんとなく「思考力だ大事だ」とは思っていても、自分一人では思考力を鍛えにくいというのが数学という科目の難しさです。
特に難関大の数学は、いわゆる「典型問題」が出題されることはほとんどなく、「思考力」を高めて解く必要があります。 独学では身に付かない思考力を「口頭試問」で高めます。
.png)
.png)
多くの場合、難関大攻略に不足しているのは、解法のストックではなく、思考力です。思考力なしでは解けない問題を使って、大学側が合格者をフィルタリングしているのです。
・今ある知識だけで解けるのに、解けないと思い込んでしまう
・答えは出せても、その根拠は理解していない
「考えたつもり」「考える作業が面倒で避ける」を防ぎ、本当に理解するまで考え抜く訓練をできるのがTHE MATHの強みです。難関大に合格する生徒は「考えたつもり」で済ますような甘い学習方法をとっていません。「考えたつもり」をなくし、学習法の水準を高めることで、難関大が求める本物の学力が手に入ります。基礎・基本を徹底し、2次試験に対応できる学力を養成する独自カリキュラムで、入塾時の学力と志望校に応じてTier.1~4の段階別に指導いたします。
.png)
口頭試問 による学習を続け、
知識・公式の 本質的 な 理解 を促す
 自信と根拠、手応えを持って問題が解ける
自信と根拠、手応えを持って問題が解ける
 応用問題にすぐに対応できる
応用問題にすぐに対応できる
 適切な表現で正確に述べる力が身に付
適切な表現で正確に述べる力が身に付
 考える癖がつくので、他の科目でも答えを導き出せる
考える癖がつくので、他の科目でも答えを導き出せる
 全教科の得点UPにつながる
全教科の得点UPにつながる
単項式・多項式・定数項の次数の定義を述べよ。
多項式ax³-3x²y + by²-cについて、x,y,xとyに着目したときの次数をそれぞれ述べよ。
「降べきの順に整理する」「昇べきの順に整理する」を説明せよ。
次の多項式をxについて降べきの順に整理せよ。
指数法則を述べよ。
(-2x²y²)³ × 5xy⁴を整理せよ。
以下の式を展開せよ。
(3a+4b)², (2a-5b)², (2a-3b)(2a+3b) をそれぞれ展開せよ。
以下の式を展開せよ。
(2a+3b)³, (2a-3b)³ をそれぞれ展開せよ。
以下の式を展開せよ。
(a-b-c)² を展開せよ。
東京大学、慶應義塾大学、名古屋大学、大阪大学、東北大学、神戸大学、北海道大学、広島大学、北里大学、久留米大学、東海大学、帝京大学、埼玉医科大学、愛知医科大学、岩手医科大学、金沢医科大学
東京大学、京都大学、一橋大学、東京工業大学、慶應義塾大学、早稲田大学、青山学院大学、
.png)
1年で日本医科大学に合格!
「理解できるまで追求する授業のおかげです」
日本医科大学 医学部医学科合格 長瀬さん(三鷹市在住/19歳男性/既卒生)
特に数学に関しては、自分が一つ答えを出すと、先生が別解を作成してくれました。参考書に書いてある解答のほかにも、さまざまな別解を教えてくれたので、一つの問題...
.png)
1年で偏差値18アップで医学部に逆転合格!
「合格から逆算する戦略がなければムリでした」
金沢医科大学医学部医学科合格 目黒さん(新潟県在住/19歳女性/既卒生)
入塾する時の偏差値は47くらいでした。自分の実力がよく分かっていないのに、「全範囲を勉強し直してから受験したい」と、今思えばわがままなことを言っていました。...
.jpg)
昭和医科大学薬学部に指定校で合格!1年半で定期テスト平均15点UP
「曖昧な理解の部分を説明できるレベルまで鍛えられました」
昭和医科大学薬学部合格 丸山さん(東京都目黒区在住/18歳女性/現役生)
元々小学5年生から通っていた塾があったのですが、あまり自主性がなく、出された宿題をこなすだけの勉強になっていました。自分の力として身についていないと感じることが増え、...
授業では生徒との口頭諮問を通して、数学の学力を高めます。問題を解いたりする時間は、自主学習がメインになります。
講師は高い指導力のプロ講師ばかりです。高い質の授業を全国どこからでも受けることができます。
東京大学 理学部数学科 卒業
最終学歴:東京工業大学(現 東京科学大学)の大学院の修士課程を修了
講師としては、学生時代から医学部・難関大専門の個別指導塾やプロ家庭教師として、10年以上指導を続けてきました。個別指導において、東京大学・慶應義塾大学・早稲田大学等の合格実績があります。
日本の高校生の数学の学力は、世界的に見てもかなり上位に位置します。確かに、基礎的な計算問題であれば、かなりの割合の生徒が解くことができます。しかし、一旦高校や大学を卒業してしまえば、多くの人が数学で習った内容を全て忘れてしまい、何のために数学を学習したのか分からなくなってしまっているような印象を受けます。
社会に出た後に、全員が必ずしも数学を必要としない職業に就くのにも関わらず、小学生の頃から高校生まで算数・数学を学校で学びます。それは数学の学習を通して論理的な思考力を養うためです。大学側としても論理的に考えることのできる学生が欲しいので、難関大であるほど思考力を必要とするような問題を出題します。ただ単に問題の解法を覚えてそれを当てはめるだけの数学の学習では、そのような問題を解けるようになることはありません。とはいえ、集団塾に通ったり、参考書を読んでみても、一人だけで思考力を高めるような学習法に辿り着くのは難しいのが現状です。
THE MATHにおいては、口頭試問を通して、自分がどこまでが分かっていて、何が分かっていないのかをはっきりさせ、数学の学習において何をすべきなのかを生徒が自覚できるような授業を行います。一人の学習においては分かった気になったつもりでも、「なぜそれが成り立つのか」を改めて聞かれると答えられない、というようなことがほとんどです。どれだけ基礎的な内容でも、それを数学的にきちんと説明できるようになるには相応の時間を必要とします。基礎・基本を重視し、まずは基本となるような内容を徹底的に理解するところから、THE MATHの授業は始まります。
.png)
私立医学部の合格実績多数
最終学歴:立命館大卒
医学部入試問題は、学校の教科書の基本問題から章末問題のようなレベルがほとんどです。しかしながら、学校の教科書の問題だけができたとしても入試に合格できるわけではありません。ではどのように勉強すれば入試に合格できるのでしょうか?
私の考えは、「基本」に素直な気持ちで勉強することだと思います。医学部浪人生の共通点としてあげられることは、まず、各々の科目の基本を定着しないでいきなり標準問題や上級問題に取り組むといったことをしているのです。基本=簡単すぎるからやりたくないみたいなプライドを持っている浪人生が多く感じます。このようなプライドを捨てて1から基本からやり直しをする癖づけや基本問題をいかにミスなく時間内に解くことを身につけられた方が意外と合格しやすいのかなと思います。
よって私の授業は、こう言った基本から徹底して授業をしていきたいと考えています。
最近の受験においては、塾や予備校が大学入試問題を分析してきたことにより、数学の入試問題もかなり研究され、ひと昔前ではかなりの難問とされてきた問題も、今では標準的なレベルとして扱われるようになりました。難関大においては典型的な問題も出題されることがありますが、一方で初見の問題が出題され続けています。いくら問題を大量に解いても、難関大で出題される問題をすべてカバーしきることは不可能です。
学校でもそのような入試問題への対策が進み、多くの中高一貫校では高校3年生になる頃には高校数学の分野を一通り学習し終えています。高校3年生になってからは、数学演習等の授業で入試問題を解く練習を続けるという、高校でも塾に負けず劣らずの対策をしています。一方で、このような入試対策を講じながらも、ほとんどの生徒が難関と言われる大学の入試で合格できるわけではありません。約1年間もの間、入試の対策をしているのにも関わらず、進学実績は例年通りになってしまいます。
このような現象が起きる理由として、「問題をやみくもに解いている」ということが挙げられます。高校の数学演習の授業で使われる問題のほとんどは入試問題ですから、それを完璧することができれば確かに数学の実力は伸びるでしょう。しかし実際には、先生が問題の解説をしてその解答を写して終わり、ということがほとんどです。それでは数学の実力が伸びるはずがありません。どれだけ入試問題を研究しても、実際に入試で出題されるのは初見の問題です。
初めて見る問題に対する思考力があるかどうかを、大学の入試では問われ続けています。
集団塾や予備校では一人の講師が複数人の生徒に対して授業をするため、一人ひとりの生徒と向き合う時間はほとんど取ることができません。生徒が個別に質問を聞きにいったり、添削指導などで生徒の答案を講師が見ることはあっても、生徒の思考を全て把握できるわけではありません。
一人ひとりの生徒と向き合うことができることが個別指導のメリットです。とはいえ、すべての個別指導塾で思考力を身に着けさせる口頭試問型の授業ができるわけではありません。現状、多くの個別指導塾ではアルバイトの大学生が講師であり、ただ解説を分かりやすく説明するだけの授業がほとんどです。生徒の思考の流れを汲み、生徒が躓いている場所に対してクリティカルな口頭試問をするのは、経験を積んだプロの講師だからこそできることなのです。
一般的に高校生は、数学の難問を複数の解法で解くところまで追求できる生徒はほとんどいません。しかし、数学の学習に必要なのは「量」ではなく「質」なのです。ただひたすらに大量の問題をこなすのではなく、一問の問題にじっくりと時間をかけ、様々な視点から問題を見る視点を養うことが、数学の実力を伸ばすための一番の近道なのです。難関大で出題されるような入試問題は一つしか解法がないことは少なく、ほとんどが複数の解法で解くことができる問題です。
THE MATHの入試問題演習では、一つの問題に対して一つの解法を提示するのではなく、そのような複数の解法の中から最も適した解法を選ぶ訓練を行います。それが、数学の能力を入試本番で縦横無尽に使えるようになり、高いレベルで数学思考力を身に着ける王道ルートです。
.png)
.png)

難関大の場合は、入学が1年遅れると約922万円(平均年収)の損失になります。ですので、金銭面を気にされるご家庭ほど、早めに受験対策することをお勧めします。また、受験学年の前から、長期的な戦略を立てることで、逃げ切り型で合格に導くこともできます。
特に高校1年生までには、受験対策を意識した数学の学習をスタートするのが王道です。
THE MATHの授業は本質的な思考力を伸ばしながら科目の成績を上げていくので、志望校は関係ありません。理系難関大&医学部受験生でなくても受講可能です。ただし、「手早く楽して点数を伸ばしたい」「定期テストでとりあえず赤点が回避できればいい」という目的で受講されるとミスマッチになる可能性が高いため、ある程度受験に対して強い意志を持っている方、本気で成績を伸ばしたい方が向いていると思います。 「難関大を受講しようか迷っている」「受講したいけど自分に向いているのか分からない」という方は、一度お問い合わせフォームからご相談ください。
・オンラインでの1:1指導に特化しています。
・難関大志望を中心とした個別指導を行っています。
現在の受講生の半数以上が他の塾にも同時に通っており、数学のみ当校にて注力しています。
THE MATHの授業は本質的な思考力を伸ばしながら科目の成績を上げていくので、志望校は関係あり ません。理系難関大&医学部受験生でなくても受講可能です。ただし、「手早く楽して点数を伸ばしたい」「定期テストでとりあえず赤点が回避できればいい」という目的で受講されるとミスマッチになる可能性が高いため、ある程度受験に対して強い意志を持っている方、本気で成績を伸ばしたい方が向いていると思います。 「難関大を受講しようか迷っている」「受講したいけど自分に向いているのか分からない」という方は、一度お問い合わせフォームからご相談ください。
メールでのご連絡やZoomを活用したビデオ面談はいつでも実施可能です。
THE MATHはグループであるASIRから派生した数学の専門コースです。ASIRが総合塾のため、数学以外の科目に関しても対応可能です。
.png)
.png)
STEP
01申し込みフォームまたは電話で承ります。希望日時を9時〜22時(土日祝日可)の間でご指定ください。
※受講可能な時間帯をできるだけ多く、ご提示ください。
例)●日16〜22時、●日18時~20時、●日10時~12時
有料体験授業は(体験55分&面談30分から選んでいただきます。最後の30分で保護者を含めた面談を行い、学習面の課題を共有させていただきます。またサービス内容が生徒に合っているのか検討できるよう、十分に説明いたします。
.png)
.png)
STEP
02保護者に各種書類の記入をしていただき、ガイダンスを行います。
春、夏、冬年3回の個別面談(各最大1時間)をご用意しております。それ以上をご要望される場合は、1回1時間あたり税込5,500円で申し受けます。
.png)
.png)
STEP
03初回授業で受験戦略の検討(有料体験授業から平均2週間以内)→ 毎週の個別指導の実施
生徒の思考力の向上や、生活習慣の実態に合わせて、戦略を調整していきます。
志望校と学力の相性を見ながら、志望校選定の戦略も作ります。年3回の個別面談を設定しています。
| コース | 対象の数学の偏差値 | 授業回数(1回120分) | 1ヶ月あたり(税込) |
|---|---|---|---|
| 偏差値20上げて 医学部・難関大突破コース |
45未満 | 週3回 | 223,500円 |
| 偏差値15上げて 医学部・難関大突破コース |
55未満 | 週2回 | 149,000円 |
| 偏差値10上げて 医学部・難関大突破コース |
60未満 | 週1回 | 74,500円 |
※高校3年生・既卒生であれば6ヶ月の継続受講が必要(受験生の直前対策として数ヶ月の受講可能)
※高校2年生であれば10ヶ月の継続受講が必要
※高校1年生であれば1年の継続受講が必要
早期に大学受験を見据え、論理的思考力を養成します。
| 対象 | 授業回数 | 1ヶ月あたり(税込) |
|---|---|---|
| 中学生 高校1年生 |
週1回/90分指導(月4回分) | 51,000円 |
| 週1回/120分指導(月4回分) | 68,000円 |

.png)

.png)
.png)
体験授業を
受けると
体験授業を 受けると



STEP 1
フォーム送信

返信メール確認
申込から平均24時間以内

体験授業&面談実施
申込から平均3〜4日後口頭試問の力で 難関大に合格できる
本物の数学力を身につけよう